Imaginary numbers seem to have something to do with time because they show up in both quantum mechanics and relativity in relationship to time. They also structure the complex plane in which many fractals manifest, such as the Mandelbrot set. Very few physicists or mathematicians however, will venture to ascribe a meaning to this mathematical formulation, which seems to have no correspondence with external reality. Before exploring some mathematicians’ more creative explorations of the of the role of imaginary numbers such as Lewis Carroll, a.k.a Charles Dodgson’s “Alice’s Adventures in Wonderland” and Wolfgang Pauli’s account of active imagination, entitled “Piano Lesson,” let’s take a look at the role imaginary numbers play mathematically.
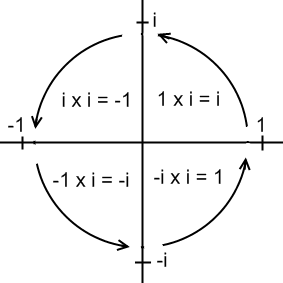 Recall that an imaginary number, i = √ – 1. Adding a vertical, imaginary axis to a real number horizontal axis creates the complex plane. A complex number is simply a combination of an imaginary number and a real number. Each point on the complex plane is described by a complex number, which is made up of an imaginary and a real component. The complex plane reveals i’s special relationship with cycles via the circle of i, also known as Wick rotation. Whenever a point on the complex plane is multiplied by i, it moves a quarter rotation around the origin or center of the plane.
Recall that an imaginary number, i = √ – 1. Adding a vertical, imaginary axis to a real number horizontal axis creates the complex plane. A complex number is simply a combination of an imaginary number and a real number. Each point on the complex plane is described by a complex number, which is made up of an imaginary and a real component. The complex plane reveals i’s special relationship with cycles via the circle of i, also known as Wick rotation. Whenever a point on the complex plane is multiplied by i, it moves a quarter rotation around the origin or center of the plane.
Applying Wick rotation to make time imaginary introduces the element of cycling, as i multiplies by itself and moves around the complex plane. This suggests a cyclic, oscillating nature of time, as it moves between the real and imaginary realms.
In quantum mechanics imaginary numbers show up in the time-dependent Schrödinger equation. Relativity’s block universe defines space-time through a 4-D Pythagorean theorem (x2 + y2 + z2 – (ict)2 = s2 ) by adding the squares of each spatial dimension and subtracting the square of time. When extracting linear time from it’s negative square, time comes out as imaginary.[1]
What might it mean for time to be imaginary? Adding an additional dimension often reveals new ways to solve problems, like the Pythagorean theorem–using 2-D squares to define a relationship between 1-D linear lengths. The imaginary axis however interacts with the real axis differently than another real axis might. Introducing an imaginary component introduces an element of cyclicity.
While imaginary numbers do not have an obvious physical interpretation, they are a powerful mathematical tool, particularly as representative of time in relativity and quantum mechanics. This seems appropriate because the experience of time feels somehow less tangible, more “in our heads,” than the spatial dimensions. While making time imaginary seems to capture some of it’s intangible nature, it also makes time easier to work with geometrically, treating it as if it were a dimension of space. Wick rotation spatializes time, by inserting the placeholder, i, for that intangibility. This works effectively in a number of scenarios, including relativity’s block universe where time crystalizes into one grand 4-D timeline. Yet the spatialization of time also grates on our common sense notion of time as flowing in one direction. When formulated as imaginary, time becomes symmetrical.
In the article “Analysis of the Relationship between Real and Imaginary Time in Physics”, physicist George Jaroszkiewicz explains
…the imaginary time formulation is a useful extension of continuous real time in the various branches of Special Relativity, General Relativity and Quantum Mechanics, but there are deep uncertainties as the the physical meaning of what is involved.[1]
These deep uncertainties, as to exactly what imaginary time means, can provoke very strong reactions in people, especially when mathematicians first started using them. Most everyone knows the story of Alice in Wonderland, but few people know that Lewis Carroll, the author, was the pen name of conservative mathematician Charles Dodgson, and that Alice’s story has marked resonances as a reductio ad absurdum critique of the increasingly abstract mathematics of the 19th century, including the use of imaginary numbers.
The Mad Hatter’s tea party, stuck in an endless rotation around the table because character of Time had left them stuck at 6 o’clock, nods to mathematician William Rowan Hamilton’s development of quaternions which required a fourth dimension of time in order to perform rotations in the complex plane.[2] In addition, Alice’s confusion as to whether “saying what she means,” means the same as “meaning what she says” mocked the non-commutative nature of Hamilton’s formulation.[3] Commutatively means it does not matter what order to do something in like in addition or multiplication. Division and subtraction are non-commutative. Which number comes first completely changes the result of the equation. 5 – 3 is not the same as 3 – 5. Hamilton’s quaternions ended up coming in quite handy in many applications, including: special and general relativity, robotics, and computation. So perhaps imaginary numbers are not as outlandish and Dodgson, a.k.a. Carroll, intended to imply.
One hundred years after 1865’s “Alice’s Adventures in Wonderland” mocked the use of imaginary numbers, they had become more commonplace in physics, though no less mysterious. Quantum physics pioneer Wolfgang Pauli recorded his reflections on the gift of the “ring of i,” in the conclusion of an exercise of “active imagination,” dialoging with the unconscious. He entitled the piece, “The Piano Lesson,” and dedicated it to psychologist Marie Louise von Franz, Carl Jung’s protégé. In the reflection he receives the “ring of i” as a gift from the piano teacher, “She.” They had the following exchange, hinting at some of the more mysterious and esoteric meanings of imaginary numbers.
I: The i makes the void and the unit into a couple. At the same time it is the operation of rotating a quarter of the whole ring.’
She: ‘It makes the instinctive or impulsive, the intellectual or rational, the spiritual or supernatural, of which you spoke, into the unified or monadic whole that the numbers without the i cannot represent.’
I: ‘The ring with the i is the unity beyond particle and wave, and at the same time the operation that generates either of these.’
She: ‘It is the atom, the indivisible, in Latin…’ When I spoke these words she gave me a significant look, but it seemed to me not necessary to say Cicero’s word for the atom aloud.[4]
I: ‘It turns time into a static image.’
She: ‘It is the marriage and at the same time the realm of the middle, which you can never reach alone but only in pairs.[5]
In this short exchange we bear witness a physicist’s dialog with his intuition, presented in feminine form, clearly articulating her own importance. Pauli, the first person speaker first describes imaginary numbers (i), making the void (the negative) and the unit (1) into a couple (i x i = -1), and performing a quarter turn of Wick rotation. She, the voice of feminine intuition whom he has entered this state to learn from, then speaks to the unquantifiable aspects of life which mathematics cannot capture without something to represent the intangible, or imaginary (i).
Pauli then describes the essential role of imaginary number in quantum mechanics and attends to the non-duality of i. Then She identifies the intangible i as the atomic unit from which all things are created, and implies this identification with the feminine body as well.[6] He points to the role of imaginary numbers as spatializing time in special relativity’s block universe.
Then She makes it explicitly relational, “It is the marriage, and at the same time the realm of the middle, which you can never reach alone, but only in pairs,” thus implying that an object, “marriage,” is never a thing, or even two things, but a relationship, the mysteriousness that arises between two—the marriage of time and space, of wave and particle, of masculine and feminine. Here she makes a case for her own necessity, for the necessity of intuition, of the feminine, of a non-dual perspective, to achieve any sort of fundamental comprehension of reality.
While mathematical physics highlights the logical conclusions of such intuitions once they have been sorted out, rarely does a physicist have the chance to publically articulate this delicate process of drawing wisdom out of the unconscious. Physicists might dismiss this passage as fruitless, unfounded speculation, but I suggest its intuitions, deeply rooted in Pauli’s profound understanding of the physics and math, offer important insights into the meaning of imaginary time, not to mention profound insight into the role of feminine and intuition as essential dialog partners.
The lack of imaginary time’s physical meaning seems to demand a more qualitative interpretation. Any phenomena with both a physical and subjective meaning lends itself to a purely physical interpretation by a scientific mindset. The lack of physical interpretation for imaginary numbers forces the scientific mindset to step outside of itself. Just as quantum mechanics, relativity, and postmodernism demands the inclusion of the conscious subjectivity of the observer in any account of knowledge, imaginary time facilitates a pervasive reminder that mathematics does not happen without some form of imagination. Imagination facilitates our view into the inner workings of reality.
What does imaginary time mean for our understanding of time then? Jaroszkiewicz focuses on how irreconcilable current interpretations of imaginary time seem to be with our experience of time.
If real time is an illusion, physics will eventually have to discuss the reasons for that (which means extending physics to include the neurosciences), whilst if real time is not an illusion, physicists still have a long way to construct a mathematically sound set of theories which do not invoke imaginary time. The third alternative is to settle for the black box recipe, which unfortunately is the position taken by many physicists.[7]
In other words, either: the effectiveness of imaginary time means time is an illusion, get rid of imaginary time, or just keep pretending imaginary time does not mean anything. A fourth possibility might allow for the co-existence of both real and imaginary time, through an understanding of the relationship between time and timelessness, and between physics and consciousness. The natural extension of Jaroszkiewicz’s argument is not the mutual exclusivity of real and imaginary time, but their complementary nature. By exploring the boundaries and relationships of these descriptions with one another, we can establish a more complete picture of time and our relationship to it.
The uses of imaginary time offer clues as to the reality of time. In special relativity, imaginary time seems to provide something of a timeless perspective, allowing us to step outside of time and space via Minkowski’s block universe. In quantum mechanics, as Wick rotation translates between the real and imaginary axis, the Schrodinger equation takes on the form of a diffusion equation and then cycles back into classical predictions.
I suggest that the complex plane itself offers a framework that interfaces timeless with the real timeline, and that Wick rotation describes oscillations between the infinite potentiality of imaginary axis’ timelesseness and manifestation in finite space-time. The progression of the oscillations between potentiality and manifestation could generate our sense of time as a linear progression within the timelessness of the present moment.
Squaring any point on the complex plane performs a quarter Wick rotation by multiplying its imaginary component by itself. Thus the squaring of imaginary time in the block universe and the Schrodinger equation’s probability amplitude facilitates their negotiation between time and timelessness.
Wick rotation seems to translate back and forth between timelessness and time, just as we do whenever we move between reflection and action. In reflective states imagination give us access to the timeless perspective of memory and possibility without the external restrictions of causal temporality. In fact, one of the distinguishing features of a timeless perspective is its overlap with temporal symmetry.
However, Jaroszkiewicz agrees that, “time is not space,” but that it works to treat it as such by making it.[8] Specifically, he means that we do not experience time as reversible; we do not seem to move to back and forth in time as we can in space. There are however, notable exceptions to this apparent “rule,” as we shall discuss in upcoming chapters.
[1] Buccheri, R., M. Saniga, and W.M. Stuckey, eds. 2003. The nature of time: Geometry, physics and perception. Dordrecht: Kluwer Academic Publishers. p 163.
[2] Contrary to Minkowski’s formulation, Hamilton described space as imaginary and time as real. The important thing seems to be that one is real and the other imaginary in order to preserve the perpendicular relationship between space and time.
[3] Bayley, Melanie. 2009. Alice’s adventures in algebra: Wonderland solved. New Scientist. Dec 19, 2009. Issue 2739. http://www.newscientist.com/article/mg20427391.600-alices-adventures-in-algebra-wonderland-solved.html?full=true#.UupxnHddW6o
[4] Though not specified by Pauli in the context of this story, I surmise that Cicero’s word for atom is corpusculum, a diminutive term for body,implying a double entendre, as it is also used in affectionate reference to the female body. (Reinhart, et al. 2005, p 159 – 162)
[5] Pauli, Wolfgang. 1953. The Piano Lesson. Harvest. Journal for Jungian Studies, 2002, Volume 48, No. 2. Trans: Frederik W. Wiegel, Herbert van Erkelens and Jos van Meurs. Retrieved from: http://herbert.vanerkelens.nl/2009/03/the-piano-lesson/
[6] See 2nd footnote back.
[7] Buccheri, R., M. Saniga, and W.M. Stuckey, eds. 2003. The nature of time: Geometry, physics and perception. Dordrecht: Kluwer Academic Publishers. p 161.
[8] Buccheri, R., M. Saniga, and W.M. Stuckey, eds. 2003. The nature of time: Geometry, physics and perception. Dordrecht: Kluwer Academic Publishers. p 153.
This is an excerpt from my forthcoming book: “The Texture of Time.”